動的計画法

ナップサック問題に関して，再帰を用いた素朴なプログラム及び動的計画法を用いたプログラムを作成し，その実行効率を確認する．発展課題では，部分和問題を動的計画法で解くプログラムを作成する．

以下のソースコードは，次のURLからダウンロードできる． * ソースコード： https://www.coins.tsukuba.ac.jp/~amagasa/lecture/dsa-files/dsa-code-dp.zip

プログラム：ナップサック問題

knapsack.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define max(a, b) (a > b? a: b)

/**
 * ナップサック問題の最適解を探索（動的計画法を用いない）
 * v: 価格の配列
 * w: 重さの配列
 * k: 対象とする荷物の数
 * i: ナップサックの容量
 */
int knapsack(int v[], int w[], int k, int i) {
  if (k == 0) return 0;

  // 関数を完成

}
int main(int argc, char** argv) {
  /* 教科書：表 6.1の例
     v[1]〜v[4]：価格
     w[1]〜w[4]：重さ */
  int v[] = {0, 250, 380, 420, 520};
  int w[] = {0, 1, 2, 4, 3};

  // 引数処理
  if (argc == 3) {
    int k = atoi(argv[1]);
    int i = atoi(argv[2]);
    if (k < 1 || 4 < k || i < 1 || 4 < i) {
      fprintf(stderr, "k と i は [1, 4] の範囲で指定してください。");
      return 1;
    }
    printf("結果：%d\n", knapsack(v, w, k, i));
  } else if (argc == 2) {
    // 荷物をランダムに生成
    int n = atoi(argv[1]);
    int* v = (int*)malloc(sizeof(int) * (n + 1));
    int* w = (int*)malloc(sizeof(int) * (n + 1));
    // 乱数の初期化
    srand((unsigned int)time(NULL));
    for (int i = 1; i <= n; i++) {
      v[i] = rand() % 101;
      w[i] = rand() % 10 + 1;
    }
    printf("容量：%d\n", n * 5);
    // 実行時間を計測
    clock_t start_clock, end_clock;
    start_clock = clock();
    int i = knapsack(v, w, n, n * 5);
    end_clock = clock();
    printf("結果：%d\n", i);
    printf("実行時間：%f sec.\n", (double)(end_clock - start_clock) / CLOCKS_PER_SEC);
    free(v);
    free(w);
  } else {
    fprintf(stderr, "Usage: knapsack <k: no. of items> [<i: capacity>]\n");
    return 1;
  }
  return 0;
}

実行方法

上のプログラムは，２つの引数(荷物の数，ナップサックの容量）を与えると，表6.1のナップサック問題に対する探索を行う．

$ ./knapsack 4 4
結果：770

ひとつの引数(荷物の数）を与えると，荷物をランダムに生成し，関数knapsackを実行し，実行時間を秒で示す．

ナップサック問題の計算時間は与えられた荷物の重さに大きく依存するが，荷物の重さがランダムで1〜10kg, ナップサックの容量が「荷物の個数」× 5kgの場合を実行する．

$ ./knapsack 5
容量：25
結果：214
実行時間：0.000005 sec.i

基本課題1

動的計画法を用いずに，下の式を直接用いて再帰的にナップサック問題の最適解を探索する関数knapsackを実装すること．選択された荷物の集合は計算しなくて良い． G_{k,i}は k 番目までの荷物に対して, ナップサックの容量を i としたときの最適解である． Gが式の右辺に現れるので再帰的な関数になる．

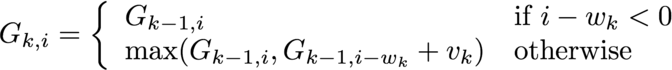
以下の要件を確認すること．

教科書の表 6.1の例に関して，荷物の数が4, 容量が3,4,5の場合の実行結果が正しいことを確認すること．
knapsack関数の実行時間が荷物の数に関して指数関数的であることを確認せよ．上のプログラムの引数として荷物の数を与え，荷物の数が25〜30の場合の実行時間を確認すれば良い．

基本課題2

動的計画法を用いてナップサック問題の最適解を探索するプログラムknapsackDPを実装すること．同定計画法を用いたknapsack関数以外の部分は上のプログラムを使うこと．教科書p.132, リスト6.3を参照するとよい．選択された荷物の集合は計算しなくて良い．

以下の要件を確認すること．

教科書の表 6.1の例に関して，荷物の数が4, 容量が3,4,5の場合の実行結果が正しいことを確認すること．
動的計画法を用いない実装よりも遥かに大きな問題を解けることを確認せよ．動的計画法による実装の時間計算量に関して，実験により議論した場合は加点する．

発展課題1

動的計画法によるナップサック問題のプログラムを選択された荷物を表示するように拡張せよ．

真偽値型の2次元配列 S [n+1][C+1] を用いて選択された荷物の集合を計算すると良い．最適解 G[k][i] を得るためにk番目の荷物を選択した場合にS[k][i]を真にし，それ以外の場合は偽とする．k-1番目までの荷物が選択されたかは，最適解 G[k][i] をどう得たかを考えれば分かる． knapsack関数は, 配列G[][]と配列S[][]から選択された荷物の集合を表す配列SS[]を計算し，配列S[]を結果として返す．

実行例

% knapsackDP2 4 5
重さ 2 価値 380
重さ 3 価値 520
合計価値 900

この実行例は，重さ3kg, 価値520の荷物と重さ2kg, 価値380の荷物が選択されていることを示している．

knapsackDP2.c

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

/**
 * 二次元int配列の生成
 * rows: 行数
 * cols: 列数
 */
int** makeIntMatrix(int rows, int cols) {
  int** matrix = (int **)malloc(sizeof(int*) * (rows + 1));
  int* array = (int *)malloc(sizeof(int) * (rows + 1) * (cols + 1));
  for (int i = 0; i < rows + 1; i++) {
    matrix[i] = array + cols * i + 1;
  }
  return matrix;
}

/**
 * 二次元bool配列の生成
 * rows: 行数
 * cols: 列数
 */
bool** makeBoolMatrix(int rows, int cols) {
  bool** matrix = (bool **)malloc(sizeof(bool*) * (rows + 1));
  bool* array = (bool *)malloc(sizeof(bool) * (rows + 1) * (cols + 1));
  for (int i = 0; i < rows + 1; i++) {
    matrix[i] = array + cols * i + 1;
  }
  return matrix;
}

/**
 * ナップサック問題の最適解を探索（動的計画法）
 * v: 価格の配列
 * w: 重さの配列
 * n: 対象とする荷物の数
 * C: ナップサックの容量
 */
bool* knapsack(int v[], int w[], int n, int C) {
  int k, i, v1;
  int** G = makeIntMatrix(n, C);
  bool** S = makeBoolMatrix(n, C);
  bool* SS = (bool*)malloc(sizeof(bool) * (n + 1));

  // 動的計画法のプログラム（配列S[][]を計算）

  // 配列G[][]と配列S[][]から選択された荷物の集合SS[]を計算

  return SS;
}

int main(int argc, char** argv) {
  /* 教科書：表 6.1の例
     v[1]〜v[4]：価格
     w[1]〜w[4]：重さ */
  int num = 4;
  int v[] = {0, 250, 380, 420, 520};
  int w[] = {0, 1, 2, 4, 3};

  // 引数処理
  if (argc == 3) {
    int k = atoi(argv[1]);
    int i = atoi(argv[2]);
    bool* S = knapsack(v, w, k, i);  
    int total = 0;
    for (int k = 1; k <= num; k++) 
      if (S[k]) {
    total = total + v[k];
    printf("重さ %d 価値 %d\n", w[k], v[k]);
      }
    printf("合計価値 %d\n", total);
  } else {
    fprintf(stderr, "Usage: knapsackDP2 <k: no. of items> <i: capacity>\n");
    return 1;
  }
  return 0;
}

以下の要件を確認すること．

教科書の表 6.1の例に関して，荷物の数が4, 容量が3,4,5の場合の実行結果が正しいことを確認すること．
配列v[], w[]を変更し荷物の個数10の場合について実行結果を確認せよ．幾つかのナップサックの容量に関して確認すること．

発展課題2：部分和問題

部分和問題を動的計画法で解くプログラムを作成せよ．次のプログラムを参考にいて良い．

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

/* 
 * 配列setが集合{3,7,11,15} を表現
 */
int set[] = {3, 7, 11, 15};
int len = 4;

/*
 * set[]: 正の整数の集合
 * n:     対象とする要素数
 * sum:   部分和
 */
bool* subsetSum (int* set, int n, int sum) {
  bool* S  = (bool*)malloc(sizeof(bool) * len);

  /* 関数を完成 */
}

int main(int argc, char* argv[]) {
  if (argc == 2) {
    int n = atoi(argv[1]);
    int k = atoi(argv[2]);
    bool* S = subsetSum(set, n, k);
    if (S != NULL) {
      printf("部分集合");
      for (int j = 0; j < len; j++)
    if (S[j])
      printf("%d ", set[j]);
    } else
      printf("条件を満たす部分集合はない．\n");
  } else 
    fprintf(stderr, "Usage: subsetsum <n> <sum>\n");

  return 0;
}

関数subsetSumは，集合を表現する配列set のn番目までの要素に対して，部分和が sum となるような部分集合を探索する．部分和が sum となる部分集合が存在するとき，部分集合を表現するbool型の配列を返す．それ以外の場合はNULLを返す．

実行例：

第１引数が対象とする要素の数
第２引数が探索する部分和

$ ./subsetsum 4 21 部分集合 3 7 11 $ ./subsetsum 4 22 部分集合 7 15 $ ./subsetsum 4 23 条件を満たす部分集合はない．

以下の要件を確認すること．

上記の実行例に関してプログラムが正しく動くことを確認せよ．
配列setを10要素程度の適当な配列に変更し，プログラムの動作を確認せよ．

提出締切

2023年2月6日（月）15:00 ※締切語の提出は認められないので注意．